The Hénon–Heiles System
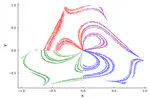
Evolution of 10,000 initial conditions, colored by which of the three exits they take from the potential.The Hénon–Heiles system is a chaotic Hamiltonian system in two degrees of freedom. It describes the planar motion of a particle in a potential $$ V(x,y) = \frac{1}{2}(x^2 + y^2) + (x^2y - \frac{1}{3}y^3). $$
It was introduced in 1964 to study the existence of additional integrals of motion in galaxy dynamics. For most initial conditions, no such integral of motion exists. Beyond a certain value of the energy, the contours of the potential function “open up” and the particle can escape to infinity through one of three exits. We are interested in tracking statistical features and geometric features of systems like this, such as e.g the time to escape as a function of initial condition. There is an extensive body of work known as transient chaos (click here for a good summary article) that describes these systems in terms of non-attracting invariant sets called chaotic saddles. I have worked on extending the class of systems to which these methods can be applied.
(To be continued)
